Pearson’s Correlation Coefficient
October 25th, 2009 | Published in Uncategorized | 2 Comments
In Toby Segaran’s book “Programming Collective Intelligence” one additional methods used “to determine the similarity between people’s interests is to use the Pearson’s correlation coefficient. In statistics Pearson’s correlation coefficient is often symbolized as simply r. I also covered Toby’s Euclidean Distance Score here.
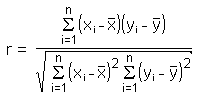
Is how r is calculated.
And here is some sloppy source code to get you going:
using System;
using System.Collections.Generic;
namespace PearsonTest
{
public class Program
{
private static void Main(string[] args)
{
var myP = new Correlation();
var lisaRose = new double[] {0, 2, 4, 6, 8, 10, 12};
var jackMatthews = new[] {2.1, 5, 9, 12.6, 17.3, 21, 24.7};
double score = myP.PearsonCorrelation(lisaRose, jackMatthews);
Console.WriteLine(score);
Console.ReadLine();
// The answer is 0.99887956534852
}
}
internal class Correlation
{
public double PearsonCorrelation(double[] x, double[] y)
{
double result;
double xMean = 0;
double yMean = 0;
double xDenom = 0;
double yDenom = 0;
double denominator;
double numerator = 0;
double n;
// Make sure arrays are same size and greater than 1
if ((x.Count() == y.Count()) && (x.Count() >= 1))
{
n = x.Count();
}
else
{
result = 0;
return result;
}
// Find Means
for (int i = 0; i <= n - 1; i++)
{
xMean += x[i];
yMean += y[i];
}
xMean = xMean/n;
yMean = yMean/n;
// Caluculate numerator and denominator
for (int i = 0; i <= n - 1; i++)
{
//Caluculate numerator
double numX = x[i] - xMean;
double numY = y[i] - yMean;
numerator += numX*numY;
// Caluculate denominator parts
xDenom += Math.Pow(numX, 2);
yDenom += Math.Pow(numY, 2);
}
// Caluculate denominator
denominator = Math.Sqrt(xDenom*yDenom);
// Check for division by zero
if (denominator == 0)
{
result = 0;
}
else
{
result = numerator/denominator;
}
return result;
}
}
}
Related Posts
AI-Powered News Aggregator for BlueskyExploring Negative r2 in Ablation Studies
Starting a Ph.D. in Computer Science
Monte Carlo Simulations in C#
Cryptanalysis Using n-Gram Probabilities