eric.ness.net

Latent Semantic Indexing (LSI) is commonly described as a “indexing and retrieval method that uses a mathematical technique called Singular Value Decomposition (SVD) to identify patterns in the relationships between the terms and concepts contained in an unstructured collection of text.”. To be a bit more clear Sujit Pal has one of the best descriptions of what LSI is and how it occures:

Latent Semantic Indexing attempts to uncover latent relationships among documents based on word co-occurence. So if document A contains (w1,w2) and document B contains (w2,w3), we can conclude that there is something common between documents A and B. LSI does this by decomposing the input raw term frequency matrix (A, see below) into three different matrices (U, S and V) using Singular Value Decomposition (SVD). Once that is done, the three vectors are “reduced” and the original vector rebuilt from the reduced vectors. Because of the reduction, noisy relationships are suppressed and relations become very clearly visible.

So how is this done?

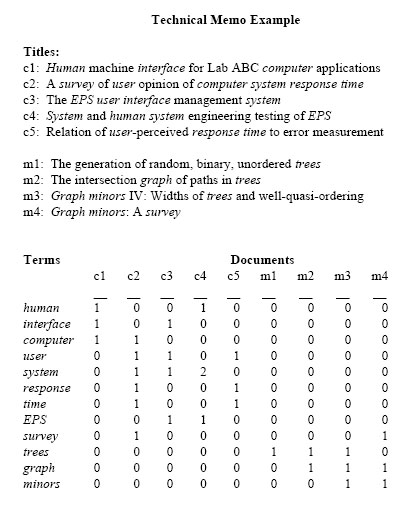
To start with let’s use the example in “Indexing by Latent Semantic Analysis” (Deerwester et al.) because you see this example repeated in a number of places on the web. The example in the paper says let’s take a look at 9 titles of papers that fall in to two categories “human computer interaction” & “graphs & trees”.

In this example the matrix is comprised of the word counts in the different document. The next step is take this matrix and break it down in to it’s different parts using SVD. The result looks like this:

After you have preformed SVD on the original matrix you then reduce the individual vectors. What the reduction of the vectors does is get rid of some of the “noise” – exposing the relationship between words and documents.

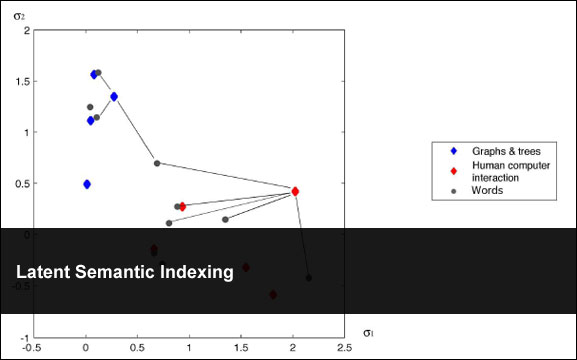
One question that arises is how much do you want to reduce the vectors (often called k)? There seems to be no hard and fast rule to this as different papers have different approaches/results with different values. In Sujit Pal’s post he uses the square root of the number of columns of the original matrix (m) which is then rounded down minus 1 which is I think a good method to use. It also happens to be the value that is used in the Deerwester paper k=2. The following picture shows what this looks like (please see Jennifer Flynn’s presentation Latent Semantic Indexing Using SVD and Riemannian SVD for a more elaborate example):

After the vectors have been reduced all that is required to do is take the vectors and multiply them back together again and that is it. See the result:

[Update: as one of the readers (Jorge) noted v is not exactly correct it should be V.Transpose. Please check out the “Indexing by Latent Semantic Analysis” (Deerwester et al.) paper starting on page 26 for the correct values of the matrices http://lsa.colorado.edu/papers/JASIS.lsi.90.pdf I will try to update this here shortly]

So lets take a look at the code – it follows the example outlined in the Deerwester paper and please keep in mind that is just a little class i put together in a asp.net test app that shows a html formatted matrix of the original (m) and the LSI result:

using System;
using SmartMathLibrary;

namespace LSITest
{
    public class lsi
    {
        // this returns the formated html results
        public string ToPrint;

        /// <summary>
        /// LISs the test.
        /// </summary>
        public void LSITest()
        {
            //Create Matrix
            var testArray = new double[,]
                                {
                                    {1, 0, 0, 1, 0, 0, 0, 0, 0},
                                    {1, 0, 1, 0, 0, 0, 0, 0, 0},
                                    {1, 1, 0, 0, 0, 0, 0, 0, 0},
                                    {0, 1, 1, 0, 1, 0, 0, 0, 0},
                                    {0, 1, 1, 2, 0, 0, 0, 0, 0},
                                    {0, 1, 0, 0, 1, 0, 0, 0, 0},
                                    {0, 1, 0, 0, 1, 0, 0, 0, 0},
                                    {0, 0, 1, 1, 0, 0, 0, 0, 0},
                                    {0, 1, 0, 0, 0, 0, 0, 0, 1},
                                    {0, 0, 0, 0, 0, 1, 1, 1, 0},
                                    {0, 0, 0, 0, 0, 0, 1, 1, 1},
                                    {0, 0, 0, 0, 0, 0, 0, 1, 1}
                                };

            // Load array in to Matrix
            var a = new Matrix(testArray);

            // print original matrix
            PrintMatrix(a);

            // preform Latent Semantic Indexing
            Transform(a);
        }

        /// <summary>
        /// Prints the matrix.
        /// </summary>
        /// <param name="myMatrix">My matrix.</param>
        private void PrintMatrix(IMatrix myMatrix)
        {
            ToPrint += "<br /><br />";

            for (int i = 0; i < myMatrix.Rows; i++)
            {
                for (int j = 0; j < myMatrix.Columns; j++)
                {
                    ToPrint += String.Format("{0:0.##}", myMatrix.MatrixData[i, j]) + "\t";
                }
                ToPrint += "<br />";
            }
        }

        /// <summary>
        /// Transforms the specified my matrix.
        /// </summary>
        /// <param name="myMatrix">My matrix.</param>
        private void Transform(Matrix myMatrix)
        {
            // Run single value decomposition
            var svd = new SingularValueDecomposition(myMatrix);
            svd.ExecuteDecomposition();

            // Put components into individual matrices
            Matrix wordVector = svd.U.Copy();
            Matrix sigma = svd.S.ToMatrix();
            Matrix documentVector = svd.V.Copy();

            // get value of k
            // you can also manually set the value of k
            var k = (int) Math.Floor(Math.Sqrt(myMatrix.Columns));

            // reduce the vectors
            Matrix reducedWordVector = CopyMatrix(wordVector, wordVector.Rows, k - 1);
            Matrix reducedSigma = CreateSigmaMatrix(sigma, k - 1, k - 1);
            Matrix reducedDocumentVector = CopyMatrix(documentVector, documentVector.Rows, k - 1);

            // re-compute matrix
            Matrix a = reducedWordVector*reducedSigma*reducedDocumentVector.Transpose();

            // print result
            PrintMatrix(a);
        }

        /// <summary>
        /// Creates the sigma matrix.
        /// </summary>
        /// <param name="matrix">The matrix.</param>
        /// <param name="rowEnd">The row end.</param>
        /// <param name="columnEnd">The column end.</param>
        /// <returns></returns>
        private static Matrix CreateSigmaMatrix(IMatrix matrix, int rowEnd, int columnEnd)
        {
            var copyMatrix = new Matrix(rowEnd, columnEnd);

            for (int i = 0; i < columnEnd; i++)
            {
                copyMatrix.MatrixData[i, i] = matrix.MatrixData[i, 0];
            }

            return copyMatrix;
        }

        /// <summary>
        /// Copies the matrix.
        /// </summary>
        /// <param name="myMatrix">My matrix.</param>
        /// <param name="rowEnd">The row end.</param>
        /// <param name="columnEnd">The column end.</param>
        /// <returns></returns>
        private static Matrix CopyMatrix(IMatrix myMatrix, int rowEnd, int columnEnd)
        {
            var copyMatrix = new Matrix(rowEnd, columnEnd);

            for (int i = 0; i < rowEnd; i++)
            {
                for (int j = 0; j < columnEnd; j++)
                {
                    copyMatrix.MatrixData[i, j] = myMatrix.MatrixData[i, j];
                }
            }

            return copyMatrix;
        }
    }
}

With much thanks to Sujit Pal, Jennifer Flynn and Deerwester for their excellent explanations.

Recommended Reading

IR Math with Java : TF, IDF and LSI – Sujit Pal

Indexing by Latent Semantic Analysis – Deerwester et al

Latent Semantic Indexing Using SVD and Riemannian SVD – Jennifer Flynn