eric.ness.net

As of late I’ve been coming across Benford’s Law all over the place and so I thought I would revisit the topic. Beford’s Law essentially states “that in lists of numbers from many (but not all) real-life sources of data, the leading digit is distributed in a specific, non-uniform way”. More specifically you should expect the leading digit ‘1’ to appear about 30.1% fo the time, ‘2’ about 17.6% and so on [see table]. One classic example for the use of Benford’s Law is in fraud detection.

One of the reasons I wanted to revisit this topic is that after having a conversation with a friend about this very topic, I came across a series of articles written by Nate Silver regarding the polling firm Strategic Vision. Strategic Vision released a poll focusing on Oklahoma students and it motivated Silver to ask a series of questions about the firm.

Now I don’t want to really focus in on all the Strategic Vision stuff but, I do want to talk about a method Silver used to detect anomalies in their polling. As Silver correctly suggests, polling would not be a good candidate to using Benford’s Law (i.e. take the last Presidential race where for the most part the two candidates were going back and forth in the 40~50% range – Benford’s wouldn’t work). However, there is another method that might give you a little insight as Silver explains:

For each question, I recorded the trailing digit for each candidate or line item. For instance, if Strategic Vision had Barack Obama beating John McCain 48-43 in a particular state, I’d record a tally in the 8 column and another in the 3 column. Or if they had voters opposing a particular policy 50-45, I’d record a tally in the 0 column (for 50) and another in the 5 column (for 45).

And what Silver says essentially is, that if you look at the last digit you should have roughly a uniform distribution. Put it another way, that if I have roughly 200 4’s I would expect roughly 200 8’s too. Silver also says that when using the trailing digit method that in some cases, you might find deviations from this distribution might be due to rounding error’s or a specific mathematical method. The trailing digit test is clearly not a sure fire way to detect fraud or anything, but just another useful tool to see if the data passes the smell test.

Silver’s insight prompted me to write some code and play around with these two methods just to see what comes up. Because I am fairly familiar with the the United Nation’s World Health Database, I thought I would run some tests using these methods. Here are the results:

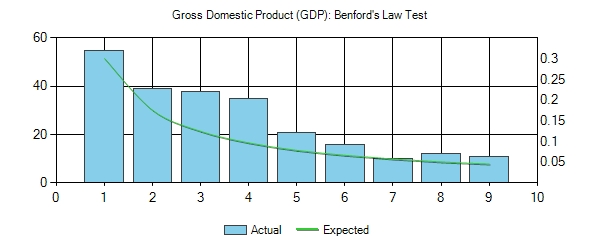
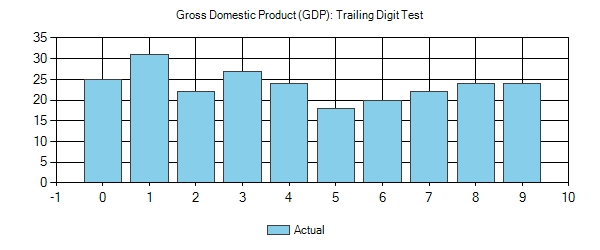
Gross Domestic Product (GDP)

As you can see, GDP generally follows Benford’s Law and the trailing digit test. Something to note on the trailing digit results – the average for each number (bin) is 23.7 so the number of 1’s and the number of 5’s are roughly equidistant from the average, even though it seems a little odd finding a GDP with a value ending in 1 is almost twice as likely as finding a value ending in 5.

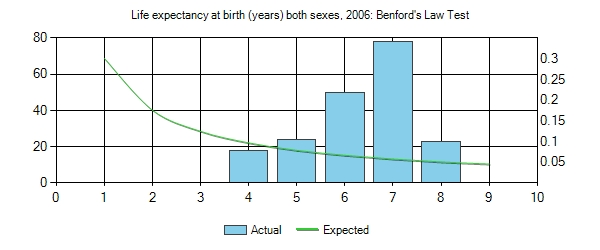
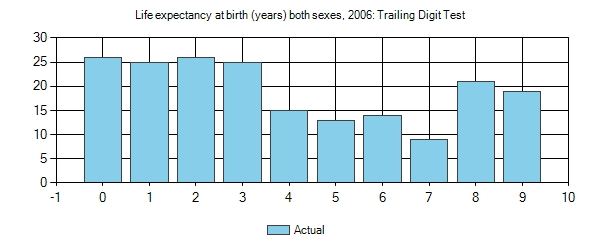
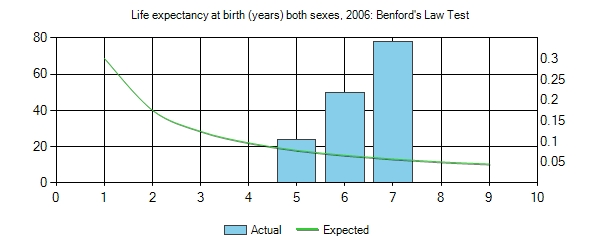
Life expectancy at birth (years)

Now here is an example where Benford’s Law will not work. The reason is because the range of life spans for all countries is from 40-83 years of age, so we are going to have to focus in on the trailing digit test.

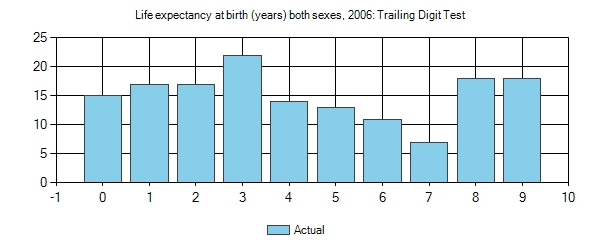
You will notice that there is something weird here with the trailing digits. First, the average value is 19.3 and we have 0’s and 2’s appearing almost 3 times more than 7’s. One thing that might account for this disparity is the fact that we have a little over 20 countries that fall in the range of 80-83, which would tilt the values of 0,1,2,3 a little higher than normal. And the number of countries in the 40’s is also a little sparse. So what I did was remove these from the set and re-ran the test. Here are the following results.

You will notice that after cleaning up the data a 3 is still almost 3 times as likely to appear as a 7 in what should be some fairly naturally occurring numbers. The average for this set is 14.8.

Now I think it would be inappropriate for me to draw any hard conclusions about the Life Expectancy data other than to say that some form of rounding has likely occurred due to the fact that the data are all whole numbers.

That said though, you can see how these two simple/practical tests can assist in determining whether there has been some human manipulation of the data. Here is the code that I used:

using System;
using System.Linq;

namespace BenfordsLaw
{
    /// <summary>
    /// Benfords Law Class
    /// </summary>
    public class Benfords
    {
        /// <summary>
        /// Adds the data.
        /// </summary>
        /// <param name="data">The data.</param>
        /// <returns></returns>
        public double[] CalculateBenfordsDistribution(double[] data)
        {
            if (data.Count() == 0)
            {
                throw new ArgumentException("Error: There are no items in your data array.");
            }

            //Create benford bins to hold counts
            var benfordsContainer = new double[9];

            // Loop through array
            foreach (double number in data)
            {
                // Get absolute value of number
                double currentNumber = Math.Abs(number);

                // for items smaller than 1 * multiply it so you
                // can find the first number
                if ((currentNumber < 1) && (currentNumber > 0))
                {
                    double num = (currentNumber*10000);
                    while (num >= 10)
                        num /= 10;
                    PackageNumberInBenfordBin(benfordsContainer, num);
                }
                else
                {
                    double num = currentNumber;
                    while (num >= 10)
                        num /= 10;
                    PackageNumberInBenfordBin(benfordsContainer, num);
                }
            }

            return benfordsContainer;
        }

        /// <summary>
        /// Trailings the digit check.
        /// </summary>
        /// <param name="data">The data.</param>
        /// <returns></returns>
        public double[] TrailingDigitCheck(double[] data)
        {
            if (data.Count() == 0)
            {
                throw new ArgumentException("Error: There are no items in your data array.");
            }

            //Create benford bins to hold counts
            var trailingContainer = new double[10];

            // Loop through array
            foreach (double number in data)
            {
                // Get absolute value of number
                double currentNumber = Math.Abs(number);
                string numTemp = currentNumber.ToString();
                string numTemp2 = numTemp.Substring(numTemp.Length - 1);
                PackageNumberInTrailingBin(trailingContainer, Convert.ToDouble(numTemp2));
            }

            return trailingContainer;
        }

        /// <summary>
        /// Packages the number in benford bin.
        /// </summary>
        /// <param name="myContainer">My container.</param>
        /// <param name="num">The num.</param>
        private static void PackageNumberInBenfordBin(double[] myContainer, double num)
        {
            // Update container totals
            int myNum = Convert.ToInt32(Math.Floor(num));
            myContainer[myNum-1] += 1;
        }

        /// <summary>
        /// Packages the number in trailing bin.
        /// </summary>
        /// <param name="myContainer">My container.</param>
        /// <param name="num">The num.</param>
        private static void PackageNumberInTrailingBin(double[] myContainer, double num)
        {
            // Update container totals
            int myNum = Convert.ToInt32(Math.Floor(num));
            myContainer[myNum] += 1;
        }
    }
}